컴퓨터의 숫자 연산

컴퓨터의 진법

우리는 컴퓨터가 2진수로 숫자를 처리한다고 많이 접했다.

어찌보면 당연한 선택이기도 하다. 메모리 셀, 플립플롭 등에 데이터를 저장하는 컴퓨터는 전하가 일정치를 넘어서 존재하느냐(1), 존재하지 않느냐(0) 외에 추가적인 선택지를 고안하기는 쉽지 않기 때문이다.

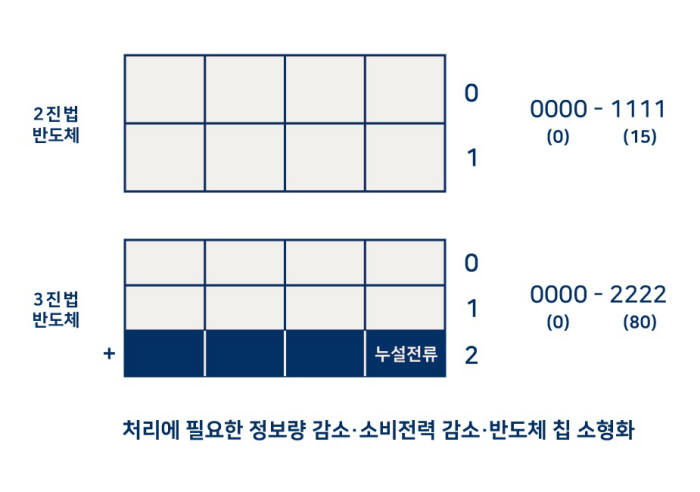
3진법으로 컴퓨터를 구성하는 개념과 시도 또한 있는 것으로 알고 있다.

몇 년 전에 한국 연구진이 발표한, 누설전류를 이용해 추가적인 상태를 나타내는 3진법 반도체 또한 그 일환이다.

하지만 여전히 우리가 사용하는 대다수의 컴퓨터는 2진법으로 구성되어 있다.

2진법은 만능일까?

우리는 10진법을 사용하며 살고 있다. 하지만 컴퓨터의 세계는 2진법이다. 여기서 숫자 표기의 괴리가 나타나게 된다.

위와 같은 원판이 존재한다고 생각해보자. 10진법은 저 원판을 10개로 나누어 생각하는 개념이고, 2진법은 2개로 나누어 생각하는 개념이다.

만약 저 원판 중 10진법으로 표기된, 10개로 나뉘어진 원판 중 하나를 2진법으로 표기하고 싶어졌다. 어떻게 해야할까? 정확한 표기가 가능할까?

한번 계속 나누어 보자.

2진법의 원판을 10진법의 조각 한 개와 같게 하기 위해 지속적으로 나누어 봤으나, 이미 몇 단계만 진행해도 같게 만들 수 없다는 사실을 깨닫게 된다.

저 과정을 범위를 좁혀가며 숫자로 정리해보자면 다음과 같다.

1. 1 / 2 = 0.5 

=> 0 ---- 0.1 ---- 0.5

2. 0.5 / 2 = 0.25

=> 0 ---- 0.1 ---- 0.25

3. 0.25 / 2 = 0.125

=> 0 ---- 0.1 ---- 0.125

4. 0.125 / 2 = 0.0625

=> 0.0625 ---- 0.1 ---- 0.125

5. 0.0625 + (0.0625 / 2)

=> 0.09375 ---- 0.01 ---- 0.0125

이처럼 우리가 쓰는 10진법과 컴퓨터의 2진법은 특정 상황에서 오차가 날 수 밖에 없는 구조이다.

그렇다면 컴퓨터 or 개발자는 어떤 방식으로 이러한 오차를 줄이거나 방지하고 있을까?

다양한 방법들

부동 소수점

이 방법은 오차를 방지한다기보다는, 효율적인 저장 기법이 더 어울리는 것 같다.

부동 소수점은 영어로 floating point(점이 둥둥 떠다닌다) 즉, 소수점의 위치가 가변적이다.

부동이 있다면 고정도 있을터, 하지만 이 방식은 각각에 할당된 크기가 고정되어 있기 때문에 아주 크거나 or 작은 수를 표현하기에는 제한적이었다.

그에 반해 부동 소수점 표기방식은 지수부와 가수부를 이용해 조금 더 유연한 표기가 가능하다. 숫자 260.5를 부동 소수점 방식으로 표기하는 예를 들어보자.

260.5(10) == 100000100.1(2)

=> 1의 바로 뒤까지 소수점을 이동시킨다
1.000001001(2) * 2^8 == 100000100.1(2)

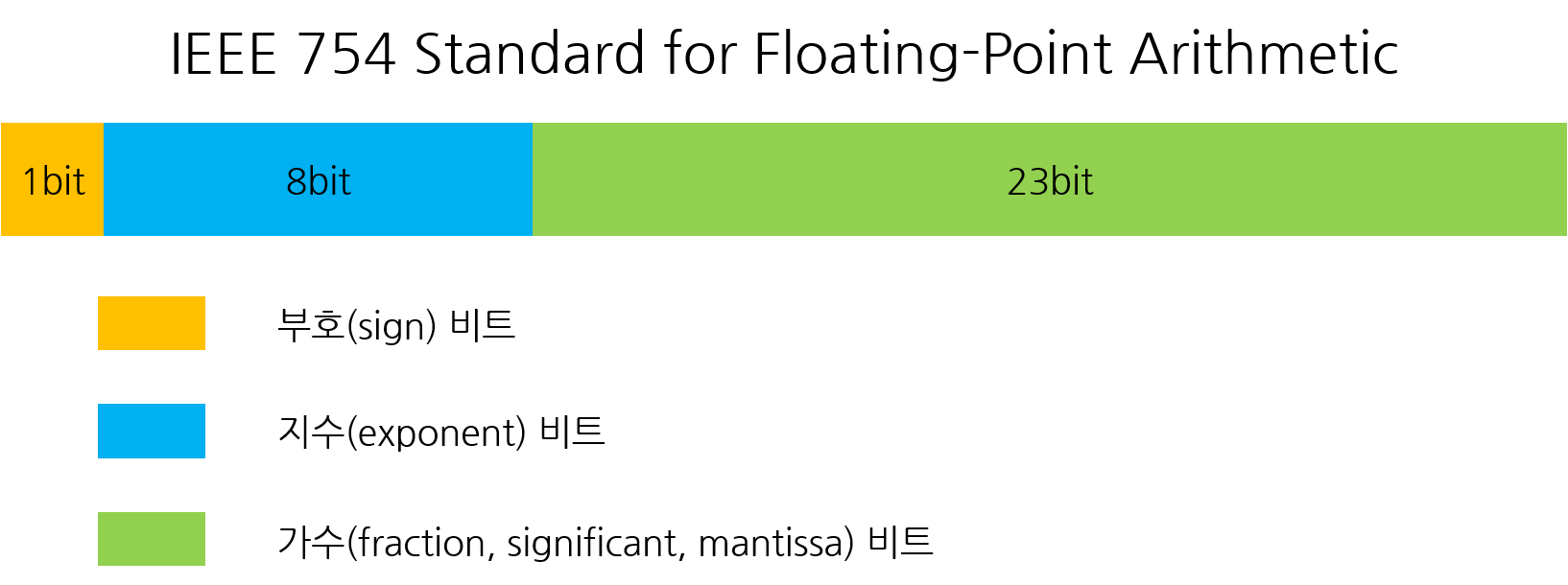
부호 (+), 지수 8

부호비트 : 0 (양수)
지수비트 : 10000111 (127 + 8 = 135) // IEEE 754 표현 방식에 따라 127을 더해줌
가수비트 : 000001001

다음과 같이 컴퓨터는 수를 계산한다.

정수 변환 계산

위와 같은 부동 소수점을 이용해도 결국 한치의 오차도 없이 계산을 하는 것은 힘들다. 그렇다면 이런 숫자 계산이 중요한 금융권이나, 코인 거래소 같은 곳들은 어떤 방식으로 문제를 해결할까?

문제가 발생하는 방식을 사용하지 않으며 해결을 했다. 무슨 말이냐면, 소수점이 발생한다면 곱연산을 해서 정수로 변환 후 처리하거나 동등한 값으로 치환을 하는 것이다.

요즘 핫한 코인의 예를 보자.

비트코인

• 분할 가능 범위 : 소수점 아래 8자리
• 0.00000001 BTC = 1 Satoshi
• 1 BTC = 100000000 Satoshi

이더리움

• 분할 가능 범위 : 소수점 아래 18자리
• 0.000000000000000001 Ether = 1 Wei
• 1 Ether = 100000000000000000 Wei

다음과 같은 방식으로 소수점으로 일어날 수 있는 문제 상황을 미연에 방지했다.

참고

• 전자신문 etnews, [KISTI과학향기]3진법 반도체를 구현하다, https://www.etnews.com/20190809000469
• 개발자 라라, 컴퓨터에서는 0.1 x 0.1 이 0.01이 아닙니다, https://www.youtube.com/watch?v=vOO-oLS0H68
• 평범한 게임 개발자, 컴퓨터의 실수 표현 방법, https://gamedevlog.tistory.com/24
• steemit, 부동 소수점(Floating Point)란 무엇인가?, https://steemit.com/kr/@modolee/floating-point