Post

정렬 알고리즘

Posted
Preview Image
By 9 min read

거품 정렬(Bubble Sort)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

public void bubbleSort(int[] arr) {

    int temp = 0;
    
    for(int i = 0; i < arr.length; i++) {   

        for(int j= 1 ; j < arr.length-i; j++) {

            if(arr[j - 1] > arr[j]) {             
                temp = arr[j - 1];
                arr[j - 1] = arr[j];
                arr[j] = temp;
            }

        }
    }
}

버블

인접한 두 데이터를 비교 후, 자리를 교환하며 정렬하는 알고리즘이다.

보통 가장 처음 배우는 정렬 방법이기 때문에 익숙하기도 한데, 바로 옆에 데이터끼리 크기를 비교하며 swap을 해주는 알고리즘이다.

시간복잡도는 최선, 평균, 최악 모두 시간복잡도가 O(n^2)으로 동일하다.

선택 정렬(Selection Sort)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

public void selectionSort(int[] arr){

    int minIndex, temp;

    for(int i = 0; i < arr.length - 1; i++){
        minIndex = i;

        for(int j = i + 1; j < arr.length; j++){

            if(arr[j] < arr[minIndex]){
                minIndex = j;
            }

        }

        temp = arr[minIndex];
        arr[minIndex] = arr[i];
        arr[i] = temp;
    }

}

selection

선택 정렬은 순서에 맞춰서 어떤 데이터를 선택할지 정하는 알고리즘이다. 자리는 이미 정해져있고, 그곳에 맞는 데이터를 찾는 알고리즘이며 다음과 같은 예시를 들 수 있다.

오름차순으로 정렬하고, 크기가 5인 배열이 있다면 0번째 인덱스에는 가장 작은 값이 와야 할 것이다. 그리고 1번째 인덱스에는 0번째 인덱스의 값보다 크고 나머지 값들보다는 작은 값이 와야 한다. 즉, 정렬 기준에 따라 자리에 맞는 값을 찾아나가는 알고리즘이다.

삽입 정렬(Insertion Sort)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

public void insertionSort(int[] arr){

    for(int i = 1; i < arr.length; i++){
        int temp = arr[i];
        int prev = i - 1;

        while((prev >= 0) && (arr[prev] > temp)){
            arr[prev + 1] = arr[prev];
            prev--;
        }

        arr[prev + 1] = temp;
    }

}

insertion

바로 앞에 있는 데이터와 대소를 비교 후, 적당한 자리에서 데이터를 뒤로 밀고 지정된 자리에 자료를 삽입하는 알고리즘이다.

오름차순 정렬 기준, 크기가 3인 배열이 있고 각 데이터의 값이 3,2,1 이라고 가정하고 비교 인덱스는 1부터 시작하니 2의 값부터 진행해보자.

1
2
3
4
5

<!-- 첫번째 -->
3. [2], 1 -> [2], 3, 1

<!-- 두번째 -->
2, 3, [1] -> 2, [1], 3 -> [1], 2, 3

다음과 같이 정렬이 진행된다.

시간복잡도는 평균과 최악(역정렬)의 경우는 O(n^2) 이며, 하지만 모두 졍럴이 되어있는 최선의 경우는 O(n)을 가진다.

병합 정렬(Merge Sort)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

public void mergeSort(int[] array, int left, int right) {
    
    if(left < right) {
        int mid = (left + right) / 2;
        
        mergeSort(array, left, mid);
        mergeSort(array, mid+1, right);
        merge(array, left, mid, right);
    }
    
}

public void merge(int[] array, int left, int mid, int right) {
    int[] L = Arrays.copyOfRange(array, left, mid + 1);
    int[] R = Arrays.copyOfRange(array, mid + 1, right + 1);
    
    int i = 0, j = 0, k = left;
    int leftLength = L.length;
    int rightLength = R.length;
    
    while(i < leftLength && j < rightLength) {
        if(L[i] <= R[j]) {
            array[k] = L[i++];
        }
        else {
            array[k] = R[j++];
        }
        k++;
    }
    

    while(i < leftLength) {
        array[k++] = L[i++];
    }
    while(j < rightLength) {
        array[k++] = R[j++];
    }
}

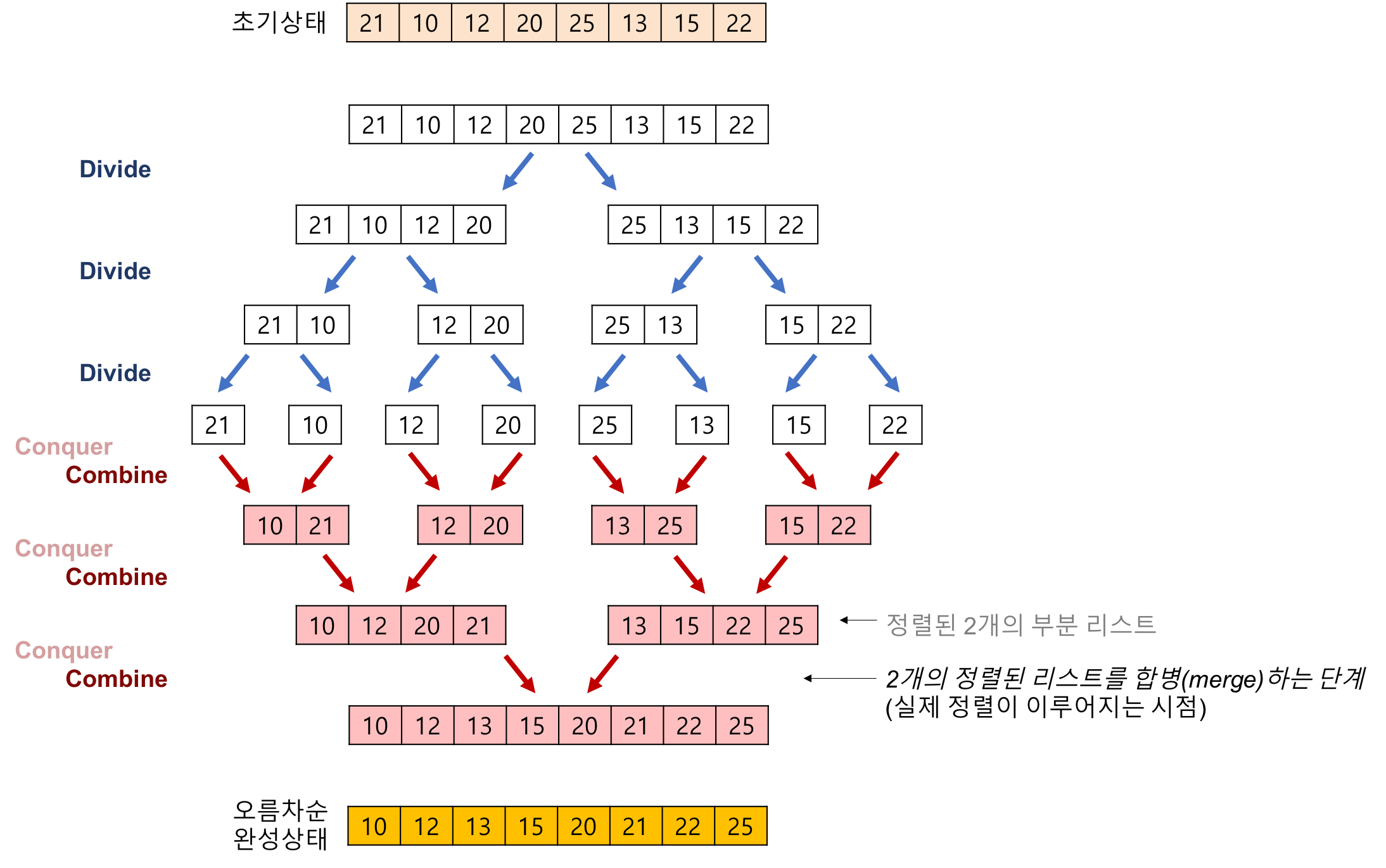
merge

데이터를 두 개의 동일한 크기로 지속적 분할, 정렬 후 작은 단위의 데이터를 다시 합해가며 전체를 정렬하는 방법이다.

데이터를 동일한 크기로 나누는 분할(divide), 나눈 데이터를 정렬하는 정복(conquer), 정렬된 작은 데이터를 다시 하나의 큰 데이터로 만드는 결합(combine)의 3단계로 이루어진다.

퀵 정렬(Quick Sort)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

public void quickSort(int[] array, int left, int right) {
    if(left >= right) return;

    int pivot = partition(); 
    
    quickSort(array, left, pivot-1); 
    quickSort(array, pivot+1, right); 
}

public int partition(int[] array, int left, int right) {

    int pivot = array[left]; 
    int i = left, j = right;
    
    while(i < j) {
        while(pivot < array[j]) {
            j--;
        }
        while(i < j && pivot >= array[i]){
            i++;
        }
        swap(array, i, j);
    }
    array[left] = array[i];
    array[i] = pivot;
    
    return i;
}

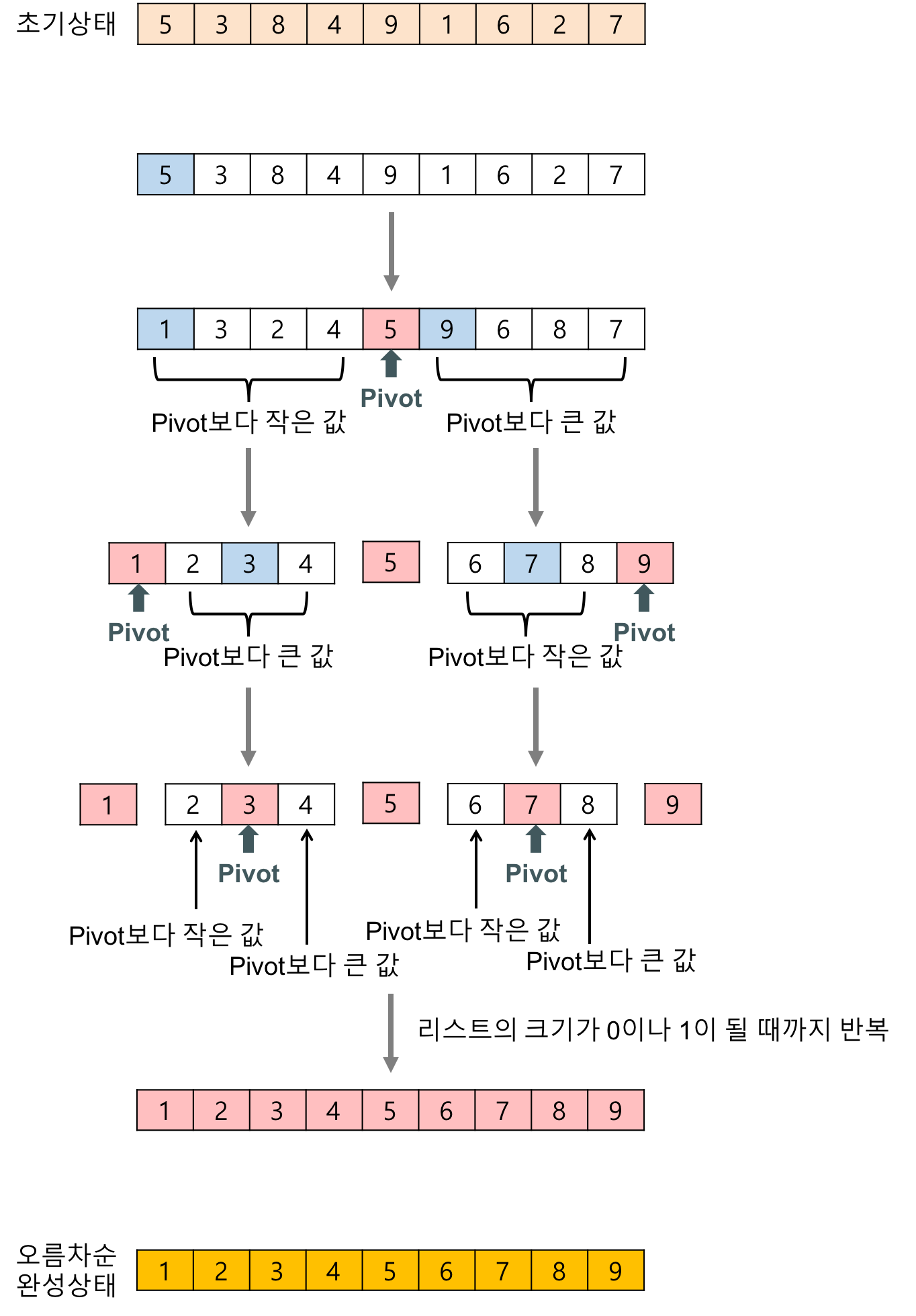
quick

퀵 정렬은 병합 정렬과 유사하지만 데이터를 비균등하게 분할한다는 차이가 있다.

먼저 기준점이 될 데이터를 임의로 한개를 선별한다. 이를 피봇(pivot)이라고 칭한다. 피봇을 기준으로 데이터를 나누는데, 오름차순 기준으로 왼쪽에는 피봇보다 작은 요소, 오른쪽에는 피봇보다 큰 요소로 나눈다. 이 과정을 분할(divide)이라고 부른다.

그리고 나누어진 데이터들을 지속적으로 정렬하는데 이를 정복(conquer) 단계라고 부른다.

병합 정렬과 마찬가지로 정렬된 작은 데이터들을 하나의 큰 데이터로 다시 합치고, 이를 결합(combine) 단계라고 칭한다

힙 정렬(Heap Sort)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

private void solve() {
    int[] array = { 230, 10, 60, 550, 40, 220, 20 };
 
    heapSort(array);
 
    for (int v : array) {
        System.out.println(v);
    }
}
 
public void heapify(int array[], int n, int i) {
    int p = i;
    int l = i * 2 + 1;
    int r = i * 2 + 2;
 
    if (l < n && array[p] < array[l]) {
        p = l;
    }
 
    if (r < n && array[p] < array[r]) {
        p = r;
    }
 
    if (i != p) {
        swap(array, p, i);
        heapify(array, n, p);
    }
}
 
public void heapSort(int[] array) {
    int n = array.length;

    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(array, n, i);
    }
 
    for (int i = n - 1; i > 0; i--) {
        swap(array, 0, i);
        heapify(array, i, 0);
    }
}
 
public void swap(int[] array, int a, int b) {
    int temp = array[a];
    array[a] = array[b];
    array[b] = temp;
}

heap

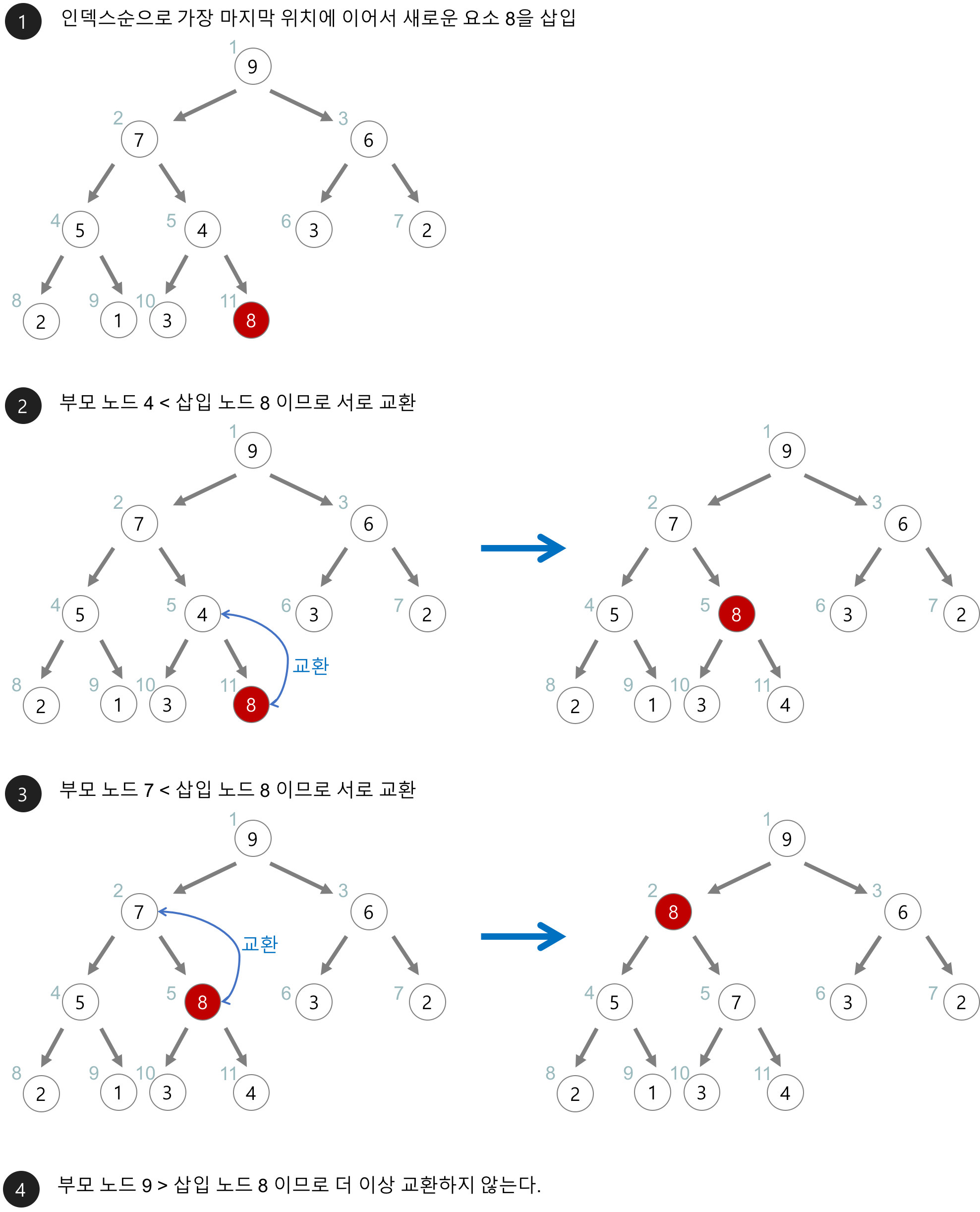
힙 자료구조를 기반으로한 정렬 방식이며, 힙은 왼쪽부터 노드가 순서대로 채워지고 서브트리의 갯수가 2개를 넘지 않는 완전 이진트리이다.

자식 노드의 값과 부모 노드의 값을 비교하며 정렬하고, 조건에 맞게 부모노드와 자식노드의 값을 교체해주는 방식이다.

참고

  • Gyuseok Kim, Tech Interview, https://gyoogle.dev/blog/algorithm/Bubble%20Sort.html
  • gmlwjd9405, 합병 정렬(merge sort)이란, https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
  • gmlwjd9405, 퀵 정렬(quick sort)이란, https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
  • gmlwjd9405, 힙 정렬(heap sort)이란, https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html
Language
This post is licensed under CC BY 4.0 by the author.

© . Some rights reserved.

Using the Jekyll theme Chirpy